Brain Constrained Neural Networks
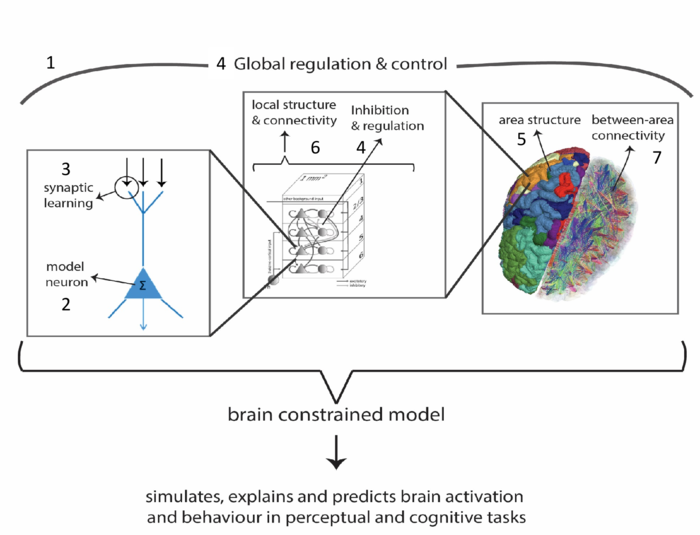
Fig. 1: The different scales of implementation for a brain-constrained neural network.
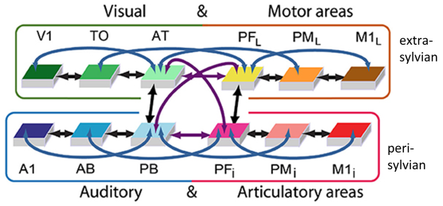
Connectivity structure of the brain constrained neural network used in MatCo.
What kind of constraints are used to make brain-constrained models more neural – as compared to most current neural networks?
To mechanistically explain the cognitive and linguistic capabilities of humans by way of computational modelling, the model needs to be similar to a real brain under a range of aspects. In the MatCo project, we use ‘brain-constrained neural networks’ – that is, computational neural networks whose architectures are constrained by how the human brain is organized and works. Which are these features? Below is a short list of examples. For a more exhaustive discussion of similarity features, see Pulvermüller et al. (2021).
Neuron model. The brain is a huge network of more than 10,000,000,000 nerve cells, which are connected with each other. Each of these neurons is a functional unit, receiving input from many others and also sending information to a different large set of similar neurons. Therefore, the functionality of neurons needs to be implemented. The neuron model used in the simulations range from mean field models to spiking or ‘integrate-and-fire’ neurons (see 2 in Figure 1).
Neural learning and plasticity. As mentioned, nerve cells connect with many other such cells. These connections can be weak or strong and importantly, they are not static but highly dynamic. Dependent on the frequency of use of a given connection, it becomes weaker or stronger. This usage-dependent plasticity is thought to be the biological basis of learning. One way of capturing learning mechanisms is to implement biologically realistic learning rules in artificial networks. We use Hebbian plasticity, which strengthens a link if the connected neurons fire together but weakens the link if either the pre-synaptic neuron or the post-synaptic neuron is silent while the other one is active. The learning algorithm also yields plasticity dependent on spike timing. (see 3 in Figure 1)
Inhibition and regulation. Activity in the brain is regulated by control mechanisms at different scales. On the microscopic level, for example, there are inhibitory cells that feed back to a range of neighboring excitatory neurons and therefore help to avoid local over-activation. At the macroscopic level, specific feedback loops in which the cortex is included (e.g., running through the basal ganglia and the thalamus) contribute to the control of cortical activity. Brain-constrained network models implement both microscopic and macroscopic mechanisms of regulation - to achieve biological plausibility. (see 4 in Figure 1)
Areas and nuclei. Whereas neurons can be microscopically small, cortical areas operate on a macroscopic scale within the realm of square centimeters. A brain-constrained network model represents areas microscopically as a collection of sparsely interconnected neurons and macroscopically as units interlinked with other such areas.(see 5 and 6 in Figure 1)
Local and long-distance connectivity. The many neurons of the cortex connect to each other by way of local connections between adjacent cells and, importantly, also by way of long-distance fiber bundles, which can even connect cells that are 10 or 20 cm apart. There is ample information from neuroanatomy about the probability of local connections and there is much recent and current research on the between-area connectivity of the human brain – the ‘human connectome’. Brain-constrained networks implement aspects of both local and long-distance connectivity to make the artificial networks more ‘brain-like’ than standard neural networks. (see 6 and 7 in Figure 1)